Dosen : Marsigit
Oleh : Siti Hanafian
Nim : 09305144034
Pelaku-palaku sejarah itu banyak, penulis-penulis sejarah itu tidak banyak, apalagi sejarah yang kaitannya dengan melakukan penelitian. Kalau mau sempurna kita menggali makam raja-raja terdahulu. Kemudian sumber-sumber yang didapat itu dipelajari, diantaranya papirus,upgrade-upgrade,dll.
Saat berbicara tentang sejarah matematika, maka yang kita juga membicarakan tentang sejarah peradaban manusia. Dari sisi sosiologi dan morfologinya manusia, sumber perdaban manusia itu dekat dengan air. Air sebagai sumber kehidupan. Manusia yang hidup di dekat muara-muara sungai yang besar memanfaatkan air untuk minum, sarana transportasi, untuk perikanan, dll.
Awalnya timbul peradaban manusia itu berasal dari persoalan-persoalan yang dihadapi manusia. Matematika itu melekat melekat pada alam dimana mereka tinggal. Saat manusia berkoloni, mereka berurusan dengan persoalan batas wilayah, yang diberi tanda, baik dengan batu maupun dengan tongkat, yang kemudian menghasilkan bangun-bangun geometri. Maka ketika manusia berkoloni, kemudian membutuhkan makanan, lalu beranak-pinak, kemudian diantara mereka ada yang menonjol, kemudian secara alami mereka berkuasa, yang kemudian mereka membentuk sistem kekuasaan yang diperintah oleh raja, yang disebut kerajaan . Lalu sungai-sungai, gurun pasir, bebatuan berkembang pesat, yang digunakan untuk keperluan upacara-upacara adat, untuk makam raja-raja, dll.
Dari daratan Afrika yang dulunya adalah dasar laut yang terangkat, dari situ muncullah peradaban-peradaban seperti Mesopotamia dan Babilonia. Kemudian setelah kebutuhan perut tercukupi, maka berlanjut pada kehidupan sosial, kemudian mereka ingin mengembangkan penemuan mereka yang mereka anggap penting untuk ditelusuri lebih jauh lagi yaitu artefak matematika.
Bangsa Mesir menarigarris tegak lurus pada pembangunan piramida kemudian mengaitkannya dengan bintang di langit. Bintang itu memiliki pola tertentu pada saat terttentu yang saat itu ia tidak mengalami perubahan. Dan susunan bintang-bintang di langit itu dipakai sebagai pedoman. Baik pedoman bagi orang yang mau bepergian, kemudian menentukan garis tegak lurus pada bangunan piramid
Di daratan Eropa matematika baru bersifat empiris, rumus-rumusnya masih berupa pendekatan angka-angka, beum menjadi rumus asli, dan rumus-rumus itu juga belum teruji, artinya ia belum tepat, masih bisa berubah-ubah.
Akhirnya bangsa Mesir bergaul dengan orang-orang Eropa. Di Eropa terdapat 4 musim yaitu panas, dingin, gugur, dan semi. Selama 3 bulan pada musim dingin yang terdapat salju, mereka bersembunyi di goa-goa atau tempat persembunyian lainnya. Mereka membuat terowongan bawah tanah, dengan kemajuan tekhnologi yang mereka miliki. Karena itu kehidupan mereka lebih berat, karena itulah tekhnolgi mereka lebih maju. Karena dari beratnya hidup mereka mereka lebih tertantang untuk selalu berkretifitas.
Dari daratan Eropa inilah muncul tokoh-tokoh matematika. Mereka berusaha membuktikan rumus-rumus matematika yang telah ada sebelumnya, menguji kebenarannya. Kemudian muncullah tokoh matematika dari Yunani bernama Thales, tetapi ia belumberhasil membuat perubahan dari rumus-rumus yang telah ada. Kemudian Pythagoras orang pertama yang membuktikan rumus segitiga siku-siku, dengan menggunakan pembuktian secara matematis, yang kemudian muncul dalil pythagoras yaitu a2+b2=c2. Sampai skarang ini telah banyak berkembang tentang pembuktian dalil Pythagoras.


Kemudian berkembang juga tentang konsep-konsep bilangan, Pythagoras sangat menghayati bilangan-bilangan ini sampai-sampai bilangan-bilangan diberi makna magic. Misalnya angka 1 sebagai lambang sesuatu, angka 2 sebagai lambang sesuatu hal juga, angka 3, dll. Karena sangat melekatnya dia dengan bilangan-bilangan ia mengatakan bilangan-bilangan itu mengatur agama. Karena dijadikan sebagai pedoman yang pada saat itu memang belum ada agama. Itu sekitar tahun 50 SM.
Kemudian muncul permasalahan tentang bumi, sebenarnya bumi itu terbuat dari apa saja. Thales berpendapat bahwa bumi itu terbuat dari air, tetapi pendapat itu tidak mutlak benar. Kemudian muncul berbagai pendapat tentang bumi, ada yang mengatakan bumi itu terbuat dari tanah, bahkan benda-benda lain.
Pada zaman Yunani terdapat banyak mitos contohnya tentang pelangi. Dikatakan bahwa pelangi adalah jembatan bagi para bidadari yang akan turun ke bumi. Lama-lama orang itu berpikir, lalu melakukan pengamatan. Pelangi muncul saat sesuadah hujan. Kemudian diketahui bahwa pelangi adalah pembiasan cahaya yang menjadi berbagai macam warna yang semula hanya berwarna putih saja. Hal ini telah merubah mitos menjadi logos.
Kemudian di Yunani juga ada tokoh bernama socrates. Pada zamannya sudah ada pemerintahan yang demokratis, ilmu pengetahuan berkembang, sudah ada doktet, guru, seniman, dll. Suatu hari Socrates memberikan pertanyaan pada seorang penggembala kambing yang buta huruf. Socrates bertanya apakah si penggembala kambing bisa mengukur luas suatu bangun. Socrates berpikir bahwa penggembala itu tidak dapat mejawab pertanyaannya karena ia buta huruf, tetapi ternyata ia salah, penggembala kambing itu bisa menjawab pertanyaannya dengan caranya sendiri walaupun ia buta huruf.
Kemudian suatu hari hari Socrates didakwa di pengadilan Athena ia dinganggap telah menyebarkan ajaran-ajaran yang menyesatkan dengan pemikiran-pemikirannya, akhirnya ia diberi pilihan dihukum mati atau dibebaskan dengan syarat tidak menyebarkan filsafat-flsafatnya lagi, maka ia memilih dihukum mati.
Socrates memiliki murid bernama Plato. Plato menulis Buku kehidupan Yunani Kuno yaitu tentang suku Celea, Athena, suku Barbar, juga tentang berbgai macam pertempuran yang dialami Yunani. Plato juga menulis Buku Republik yang berisi tentang tanya jawa Socrates dengan para ahli. Pelajaran yang didapat Socrates adalah betapa berharganya ilmu.
Menurut Plato matematika itu ada dalam pikiran kita masing-masing. Contohnya bilangan 2, 2 itu hanya ada dalam pikiran kita masing-masing. Matematika adalah sebuah ide. Menurutya peraga hanyalah sebuah contoh, itu bukan matematika, contohnya pada angka 2 tadi, 2 itu ada dalam pikiran kita dan bentuk 2 hanyalah peraga saja. Cara mempelajari matematika yaitu dengan abstraksi dan idealisasi. Abstraksi yaitu mempelajari hal-hal yang penting saja, sedangkan idealisasi adalah menganggap sempurna sifat yang ada seperti halnya pada segitiga yang lurus betul-betul lurus, lancip benar-benar lancip. Maka menurut Plato matematika itu sudah lengkap dalam pikiran kita masing-masing. Hanya saja tidak setiap orang sempat belajar matematika, karena pikirannya dipenjarakan oleh badannya.
Hakikat matematika menurut Plato adalah pengalaman. Akan tetapi menurut Aristoteles yaitu murid Plato matematika itu real, nyata, konkrit. Jadi Plato adalah orang yang idealis karena memandang matematika sebagai ide dan Aristoteles itu sebagai orang yang realis, karena menurutnya matematika itu nyata.
Pada mahsiswa perguruan tinggi matematika adalah ide. Sedangkan bagi para siswa SD, SMP, SMA matematika adalah pengalaman.
Kemudian matematika berkembang pada zaman pertengahan. Pada zaman ini terdapat suatu masa kegelapan yaitu zaman kegelapan bagi matematika. Saat itu dikuasai oleh gereja, yaitu tidak membuat kebenaran yang tidak disetuui oleh gereja, semua harus disetujui oleh gereja. Pada zaman itu dikatakan bahwa bumi adalah pusat tata surya. Kemudian dengan mengamati gejala alam Copernicus menemukan fakta yang sebaliknya yaitu matahari adalah pusat tata surya dan bukanlah bumi. Karena dianggap menentang gereja akhirnya copernicus ditangkatap berserta para pengikutnya termasuk Galileo.
Kemudian pada zaman modern orang-orang mulai memberontak dominasi kebenaran dari gereja, mereka berpendapat baha kebenaran adalah hak masing-masing orang . Dari zaman modern inilah banyak bermunculan tokoh-tokoh matematika. Contohnya Brednis yang menemukan limit dan kalkulus, Newton juga menemukan kalkulustetapi agak berbeda, Archimedes yang membahas tentang luas daerah di bawah krva lengkung, Euclides yang membahas tentang geometri aksiomatik yang dibahas dalam bukunya ”Element”, setelah itu geometri non Euclides yang membahas tentang postulat yang bermasalah pada geometri Euclides, Decrates dengan matematika dan rasio, David Young yang men gatakan bahwa matematika adalah pengalaman, kemudian muncul masala yang mempermasalahkan bahwa matematika adalah logika yang bertentangan dengan pendapat bahwa matematika adalah pengalaman. Akhirnya muncul tokoh pendamai Emanuel Kant menggabungkan antara rasio (logika) dan pengalaman, matematika adalah memang rasio tetapi juga tidak boleh melupakan pengalaman.
Orang yang pertama kali membangun sistem matematika adalah Hillbert, dalam bentuk sistem formal. Kemudian berkembanglah diantaranya terdiri dari struktur aljabar, geometri, topologi, teori group, dalam bentuk matematika aksiomatik yang pada dasarnya didahului dengan asumsi kemudian membentuk teorema.
Kemudian murid dari Hillbert yang bernama Goodel berpendapat bahwa matematika itu lengkap tetapi tidak konsisten. Lalu ia memperkenalkan Teori Kelengkapan dan tidak lengkap. Setelah itu, Widgen Stain yang menganggap matematika adalah sebagai bahasa.

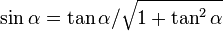
 . dan
. dan 
